Características o propiedades de las funciones

Mencionamos aquí una serie de características que pueden poseer las funciones:

Haciendo click en cada propiedad, se puede ver la definición y algunos gráficos representativos.

Estas definiciones serán usadas en las demás secciones del sitio, y deberán aplicarse en las actividades.
 
Suryectividad (ó sobreyectividad)
 

Dada una función f: A ® B, se dice que es suryectiva, si su codominio coincide con el conjunto de llegada.

Esquemáticamente:

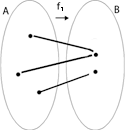
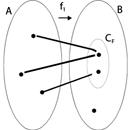
f1: A ® B  no es suryectiva

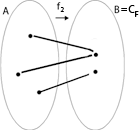
f2: A ® B es suryectiva

     Gráficamente:

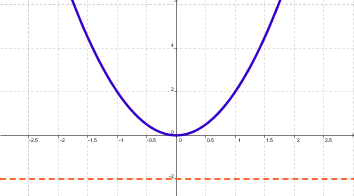
La función f:R ® R / f(x) = x2, no es suryectiva porque existe al menos un valor de y negativo que no tiene preimagen

volver al indice

 
Inyectividad
 

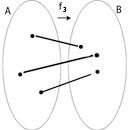
Dada una función f: A ® B, se dice que es inyectiva, si a elementos distintos del dominio le corresponden imágenes distintas.

Esquemáticamente:
 

 

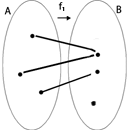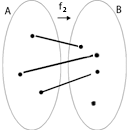f1: A ® B  no es inyectiva: existe un elemento en B que es imagen de dos elementos de A.

f2: A ® B  es inyectiva: no existen  elementos en B que sean imagen de dos elementos de A

  Gráficamente:

 

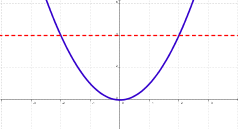f1: A ® B  no es inyectiva: existe un elemento en B que es imagen de dos elementos de A.

f2: A ® B  es inyectiva: no existen  elementos en B que sean imagen de dos elementos de A

volver al indice

 

Biyectividad

Dada una función f: A ® B, se dice que es biyectiva, si es inyectiva y suryectiva a la vez.

Esquemáticamente:

f1: A ® B no es biyectiva:
no es inyectiva

f2: A ® B no es biyectiva:
no es suryectiva

f3: A ® B  es biyectiva:
es a la vez suryectiva e inyectiva

   Gráficamente:

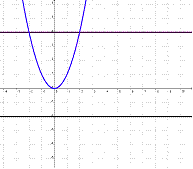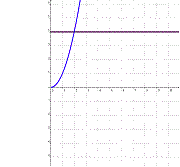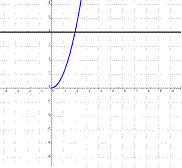
f: R ® R / f(x) = x2,
no es biyectiva, porque no
es suryectiva ni inyectiva.

f: R0+ ® R / f(x) = x2,
no es biyectiva, porque no
es inyectiva.

f: R0+ ® R0+ / f(x) = x2,
es biyectiva.
 

volver al indice
 

Paridad

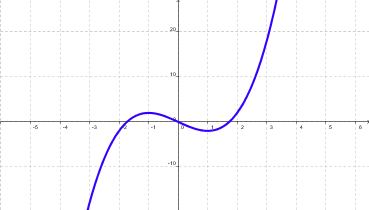
Dada f: A ® B función escalar, se dice que f es par, si:

"xÎ Df, $ -xÎ Df / f(-x) = f(x)

Gráficamente, se puede observar que una función par es simétrica con respecto al eje y:
 

 

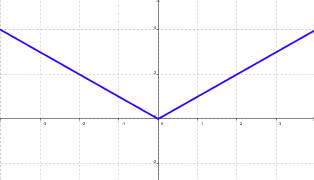
Dada f: A ® B función escalar, se dice que f es impar, si:

"xÎ Df, $ -xÎ Df / f(-x) = -f(x)

Gráficamente, se puede observar que una función impar es simétrica con respecto al origen de coordenadas:
 

volver al indice

 

Periodicidad

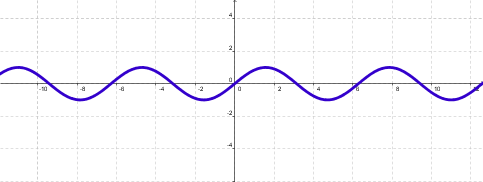
Dada f: A ® B función escalar, se dice que f es periódica, si:

$  p Î R+ / "x: x Î Df , f(x) = f(x+p)

El período de f es el mínimo valor de p para el que se cumple la igualdad.

Gráficamente, se puede observar que una función periódica se puede construir a partir de una mínima parte de su gráfica, que es la que se repite:
 

volver al indice

 
Crecimiento
 

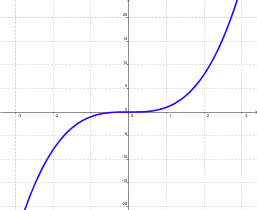
Dada una función f: A ® B, se dice que es estrictamente creciente en un intervalo, si y sólo si " x1, x2 pertenecientes al intervalo:

 x1 < x2  Þ  f(x1) < f(x2)

El intervalo puede ser abierto o cerrado.

Dada una función f: A ® B, se dice que es estrictamente decreciente en un intervalo, si y sólo si " x1, x2 pertenecientes al intervalo:

 x1 < x2  Þ  f(x1) > f(x2)
 

 

 

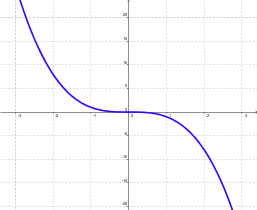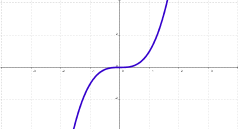
Esta función es estrictamente creciente en los reales.

Esta función es estrictamente decreciente en los reales

volver al indice