Definición de función

¿Qué es una función?

La temperatura a la que hierve el agua depende de la altura sobre el nivel del mar,
el interés que se paga por un préstamo depende del tiempo en que se pague,
el área de un círculo depende de su radio.

En todos los casos decimos que un valor “depende” de otro o “es función de” otro. Formalmente una función se define:

Dados dos conjuntos A y B no vacíos, se llama función f de A en B y se indica

f: A ® B

a toda relación de A en B en la que se verifica que a cada elemento perteneciente a A, le corresponde un único elemento perteneciente a B. A es el dominio de la función y B es el conjunto de llegada.

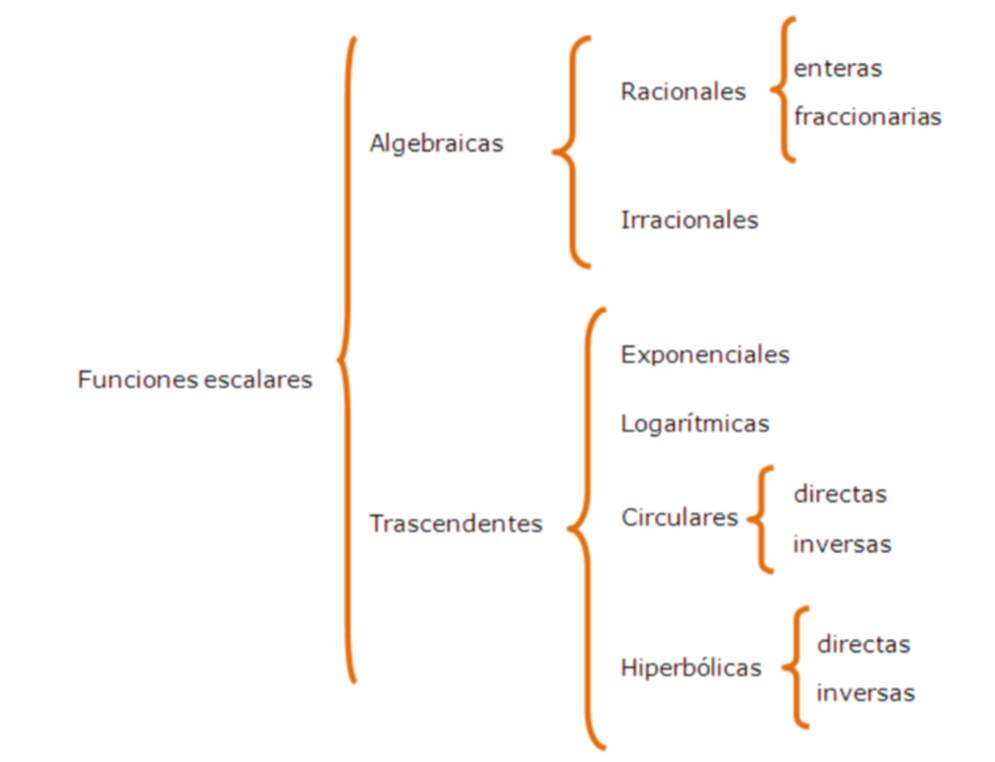
Para el estudio de Análisis Matemático I, interesan especialmente aquellas funciones cuyo dominio y codominio son subconjuntos de números reales. Se llaman funciones reales de una variable real o funciones escalares. Es decir

En esta expresión, x indica la variable independiente, e y la variable dependiente. Cuando y₀ = f(x₀), se dice que y₀ es la imagen de x₀ mediante f, y que x₀ es la preimagen de y₀ mediante f.

Clasificación de las funciones

Según las expresiones que intervengan en la ley de una función escalar f: A ® B /
A ÍR y B Í R, las funciones que estudiaremos, se pueden clasificar de la siguiente manera:

Si las operaciones algebraicas sobre la variable independiente son racionales (adición, sustracción, multiplicación, división o potenciación con exponente entero), la función se llama algebraica racional, si la variable está afectada por una raíz o exponente fraccionario entonces es algebraica irracional.
Si las operaciones algebraicas racionales son enteras (adición, sustracción, multiplicación o potenciación con exponente natural), la función se llama algebraica racional entera o función polinómica. Si la variable está dividiendo o afectada por un exponente entero negativo, es algebraica racional fraccionaria.
Se llaman trascendentes a las funciones que no son algebraicas, por ejemplo:

y = sen(x)
y = ln(x)
y = e^x
y = cosh(x)