Ciertas combinaciones de las funciones exponenciales ex y e–x, se presentan con frecuencia en matemática y sus aplicaciones, por lo que se identifican con nombres especiales.
Se definen:
| Seno hiperbólico |
|
| Coseno hiperbólico |
|
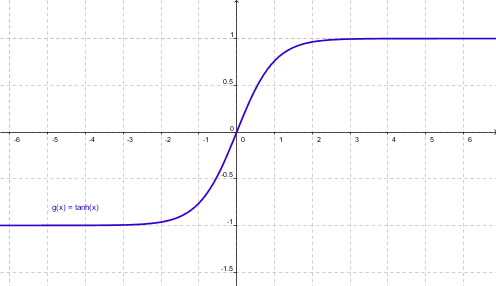
| Tangente hiperbólica |
|
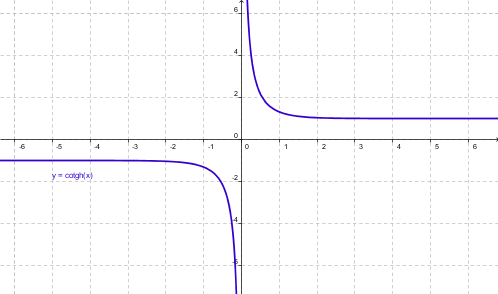
| Cotangente hiperbólica |
|
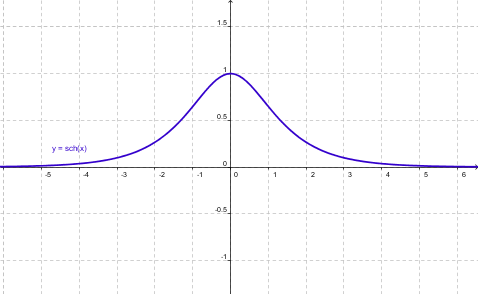
| Secante hiperbólica |
|
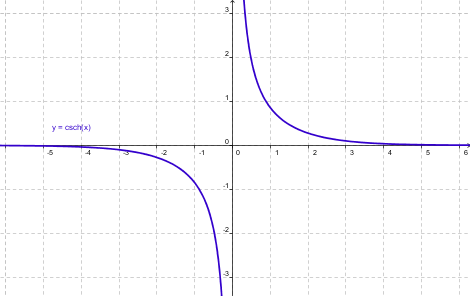
| Cosecante hiperbólica |
|
Como se puede apreciar, todas son funciones de ex y de e-x y deben su nombre a que están relacionadas con la hipérbola al igual que las trigonométricas o circulares con la circunferencia.
Las gráficas del seno y coseno hiperbólicos se pueden trazar empleando la suma gráfica de funciones como se muestra a continuación.

Observen, en la siguiente gráfica interactiva, que
cada punto de la gráfica de y = senh(x) se obtiene sumando las imágenes de y = ex
y de y = - e-x y luego dividiendo por 2.
Es decir, resulta senh(x) =
(ex - e-x)/2.
|