Por ser cualquier función un caso particular de relación, la definición dada para relación inversa sigue valiendo para la inversa de una función.
En el caso de que la función sea biyectiva, la relación inversa también será función. Entonces:
|
Si f: A ® B es una función biyectiva, la función inversa de f, que llamamos f-1, estará definida por: f-1: B® A /f-1(u) = w si y sólo si f(w) = u |
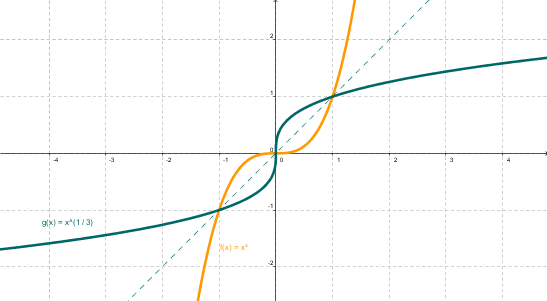
Una propiedad interesante es que la gráfica de la función inversa es simétrica a la gráfica de la función con respecto a la recta y = x. Esta simetría se observa claramente cuando se utiliza una escala 1:1 para los ejes.
Ejemplos:
-
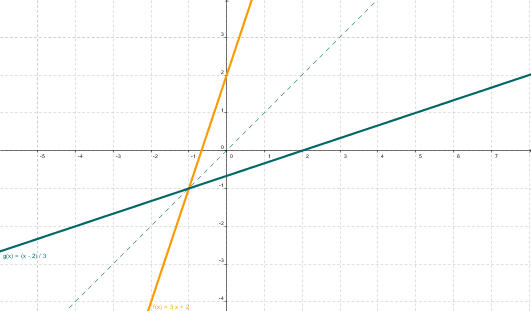
Una función lineal de pendiente no nula es biyectiva, por lo tanto tiene inversa.
-
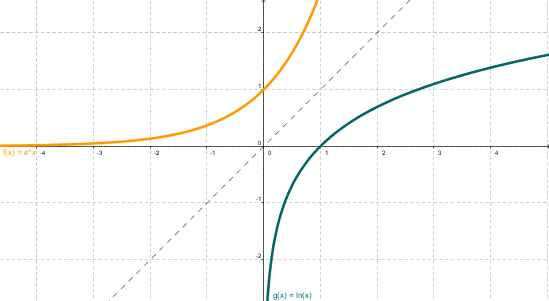
La función exponencial, tomando como conjunto de llegada los reales positivos, es biyectiva. Su inversa es el logaritmo.
-
La función f(x) = x3, en los reales, es biyectiva. Su inversa es la raiz cúbica de x.