Funciones trigonométricas

La siguiente tabla fue extraída del sitio  de Manuel Sada,

http://docentes.educacion.navarra.es/msadaall/geogebra/index.htm

Haciendo click en los diferentes vínculos se podrán ver en forma animada la generación de las curvas de las funciones trigonométricas seno, coseno y tangente, entre otras cosas.

Vean y analicen en particular los vínculos correspondientes a:

  • función seno 

  • función coseno

  • función tangente

 

Manuel Sada (Mayo 2005)

Razones trigonométricas de un ángulo agudo

Tangente de un ángulo agudo
Seno de un ángulo agudo
Coseno de un ángulo agudo
Razones trigonométricas de un ángulo agudo

Grados y radianes Radianes y grados
Función seno Función seno
Circunferencia goniométrica: seno y coseno de cualquier ángulo Circunferencia goniométrica
(seno y coseno de cualquier ángulo)		 Función coseno Función coseno
Tangente de cualquier ángulo Tangente de cualquier ángulo Función tangente Función tangente
Relaciones entre las rr.tt. de ángulos de distintos cuadrantes

Relaciones entre las razones trigonométricas de algunos ángulos:
Ángulos opuestos
 Ángulos suplementarios
 Ángulos que difieren en 180º
 Ángulos complementarios
 Ángulos que difieren en 90º

Función sinusoidal
 
En el gráfico que sigue se puede ver la función y = A sen(B.x-C).
Si los valores de los deslizadores, son A = 1, B = 1, C = 0, la función graficada es y = sen(x).

Grupo Ingeniería & Educación, Creación realizada con GeoGebra 

Las características de esta función, con los deslizadores en la posición inicial, son las siguientes:

  • Amplitud: A = 1 (altura de la onda)

  • Pulsación: B = 1 (cantidad de ondas en 2 p)

  • Período: 2 p/B = 6.28 (longitud de onda)

  • Ángulo de fase: C/B = 0 (desfasaje)

 

  1. Muevan el deslizador A y observen qué varía en la gráfica de la función y = sen(x).

  2. Ahora, luego de volver el deslizador A, a la posición A =1, muevan el deslizador B y analicen qué varía.

  3. Vuelvan el deslizador B a la posición B=1 y muevan el deslizador C. ¿Qué cambia?

  4.  Ubiquen los deslizadores en: A=2, B=3 y C= 0 y analicen:

  1. ¿Cuál es el codominio? ¿Qué relación tiene con A?
  2. ¿Cuántas ondas completas entran entre 0 y 2p?
  3. ¿Cuál es la longitud de una onda?
  4. ¿Cuál es el período?

 

Funciones trigonométricas inversas
 

Las funciones trigonométricas son periódicas así que no son biyectivas por lo tanto hay que restringir el dominio y el conjunto de llegada para que lo sean.

  •  En el caso de la función sen x, el dominio se restringe al intervalo  [-p/2, p/2] y el conjunto de llegada al intervalo  [-1, 1]

  • Para la función cos x, el dominio se restringe al intervalo  [0, p] y el conjunto de llegada al intervalo [-1, 1].

  • Para la función tg x se considera como dominio el intervalo abierto ]-p/2, p/2[ y como conjunto de llegada, los reales.

A continuación, se muestra la gráfica de cada una de estas funciones, y su inversa, marcando en el gráfico la simetría que existe respecto de la recta y = x.

 
Inversa del seno: función arcoseno

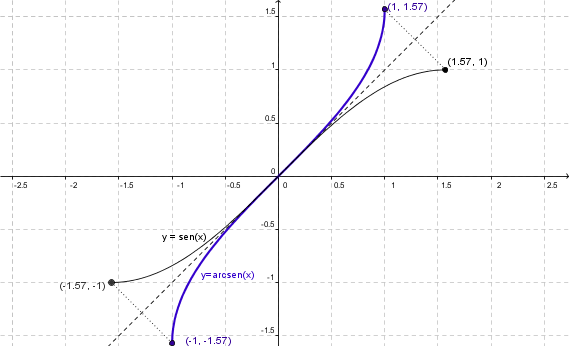
Dada , f:  [-p/2, p/2] ® [-1, 1] / y = sen(x), resulta biyectiva, entonces la función definida por

f-1: [-1, 1] ® [-p/2, p/2]  / y = arcsen(x)

es la función inversa, que también resulta biyectiva. Su gráfica es la que sigue:

 
Inversa del coseno: función arcocoseno
 

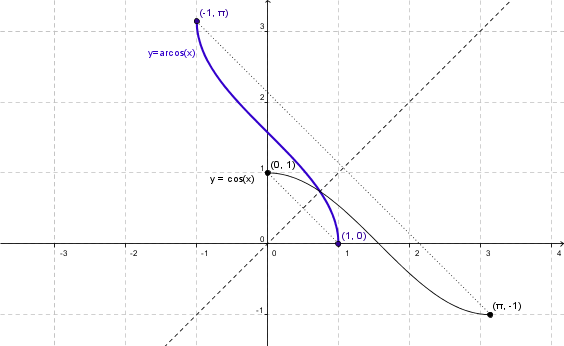
Dada , f:  [0, p] ® [-1, 1] / y = cos(x), resulta biyectiva, entonces la función definida por

f-1: [-1, 1] ® [0, p]  / y = arccos(x)

es la función inversa, que también resulta biyectiva. Su gráfica es la que sigue:

 

 
Inversa de la tangente: función arcotangente
 

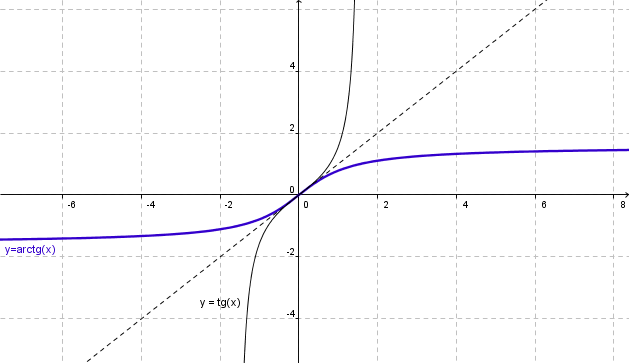
Dada , f:  ]-p/2, p/2[ ® R / y = tan(x), resulta biyectiva, entonces la función definida por

f-1: R ® ]-p/2, p/2[  / y = arctan(x)

es la función inversa, que también resulta biyectiva. Su gráfica es la que sigue: