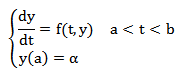ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN
Definición:
Una ecuación diferencial ordinaria (EDO) es una ecuación que relaciona
una función de una sola variable independiente y sus derivadas respecto
de esa variable.
Como es habitual indicaremos las derivadas de la siguiente manera: y’(x), y’’(x). Cuando la variable independiente es el tiempo se acostumbra utilizar un punto en lugar del apóstrofe.
Definición:
El orden de una EDO es el orden de la
derivada de mayor orden presente en la ecuación.
La EDO general de primer orden se escribe como indica la
ecuación (1)
|
y’(x) = f(x, y) |
(1) |
Una ecuación de orden n se escribe, en
forma general, según indica la ecuación (2)
|
an y(n) + an-1 y(n-1) + . . . + a1 y’ + a0 y = F(x) |
(2) |
donde la notación y(n) indica derivada de orden n, y así sucesivamente.
Las EDOs pueden ser:
-
lineales a coeficientes constantes, por ejemplo y’ + 3 y = f (x),
-
lineales a coeficientes variables, por ejemplo y’ + 2 x2 y = f (x),
-
no lineales, por ejemplo y’y + 5 y = 0 ó (y’)2 + 2 y = 0,
Definición:
La solución de una ecuación diferencial
ordinaria es una función que satisface la ecuación y las
correspondientes condiciones suplementarias en el dominio de interés.
Hay dos tipos diferentes de problemas que involucran ecuaciones diferenciales ordinarias, dependiendo del tipo de condiciones suplementarias que se especifiquen. Si las condiciones suplementarias se especifican para el mismo valor de la variable independiente el problema se llama Problema de Valor Inicial (PVI).
Si las condiciones suplementarias se especifican para dos valores de la variable independiente, el problema se denomina Problema de Frontera.
Es importante saber si cambios pequeños en el enunciado de un PVI introducen cambios igualmente pequeños en la solución, debido a los errores que puede acarrear la modelización de un problema físico, y también por la aparición de errores de redondeo al recurrir a métodos numéricos.
Un problema de valor inicial de primer orden está conformado por una ecuación diferencial ordinaria de primer orden, y una condición inicial, como se muestra en la ecuación (3):
|
|
(3) |
Definición:
Se dice que una función f(t, y) satisface una condición de
Lipschitz en la variable y, en un conjunto D si existe una
constante L > 0 con la propiedad:
|
|
(4) |
siempre que (t, y1), (t, y2) Î D. A la constante L se le llama constante de Lipschitz para f.
Ejemplo: Si D = {(t, y)/ 1 ≤ t ≤ 2, -3 ≤ y ≤ 4} y f(t, y) = t |y|,
entonces se cumple, para cada par (t, y1), (t,y2) Î D,
|f(t, y1) - f(t, y2) |= |(t |y1| - t |y2|)| = |t| |(|y1|-|y2|)| ≤ 2 |y1 - y2|
Por lo tanto, f satisface una condición de Lipschitz en D en la variable y con la constante de Lipschitz igual a 2.
Teorema:
Si f(t, y) está definida en un subconjunto convexo D de R2, y
existe una constante L > 0 tal que |∂f/∂y| ≤ L para todo (t, y)
Î D,
entonces f satisface una condición de Lipschitz en D en la variable y
con la constante de Lipschitz L.
Recordemos que un conjunto es convexo cuando dados dos puntos
cualesquiera del conjunto, el segmento que los une está íntegramente
contenido en el conjunto. En general, los conjuntos que se trabajan aquí
son rectángulos, por lo tanto son convexos. Este teorema nos da una
condición suficiente para que una función satisfaga una condición de
Lipschitz, que en general es más fácil de verificar, que la condición
misma. Cabe aclarar que no es una condición necesaria.
El siguiente teorema da las condiciones que debe cumplir un PVI de
primer orden para poseer solución única.
Teorema:
Supongamos que D = {(t, y)/ a ≤ t ≤ b, -∞ ≤ y ≤ ∞}, y que f(t, y) es
continua en D. Si f satisface una
condición de Lipschitz en D en la
variable y, entonces el problema de valor inicial y' = f(t, y), a ≤ t ≤ b,
y(a) = α,
tiene una solución única y(t) para a ≤ t ≤ b.
Ahora que ya sabemos cuándo un PVI tiene solución única, vamos a dar una serie de conceptos que permitan determinar cuándo pequeños cambios en un problema dan lugar a pequeños cambios en la solución.
Definición:
Se dice que un problema de valor inicial de tipo (3), es un
problema bien planteado si:
1.- El PVI tiene solución única, y(t).
2.- Para cualquier ε > 0, existe una constante positiva k(ε), con la
siguiente propiedad:
Siempre que |ε0 |< ε y δ(t) es continua, con |δ(t)|< ε
en [a, b], el problema
|
z' = f(t, z) + δ(t), a ≤ t ≤ b
|
(5) |
tiene una solución única z(t), con |z(t) - y(t)|< k(ε) ε, para toda a ≤ t ≤ b.
Al problema (5) se lo llama problema perturbado asociado al problema original (3), y supone la posibilidad de que haya un error en la formulación de la ecuación diferencial y en la condición inicial.
Los métodos siempre trabajan con un problema perturbado, porque cualquier error de redondeo introducido altera el problema original. Y si este último no está bien planteado, la solución numérica obtenida no aproxima con precisión a la solución del problema original.
Teorema:
Sean D = {(t, y)/ a ≤ t ≤ b, -∞ ≤ y ≤ ∞} y f(t, y) continua en D
que satisface la condición de Lipschitz en la variable y en
el conjunto D. Entonces el problema de valor inicial y' = f(t, y), a ≤ t ≤ b, y(a) = α,
estará bien planteado.
Se ve entonces que la condición de Lipschitz para la función asociada a un PVI de primer orden es una condición suficiente para que el problema esté bien planteado.