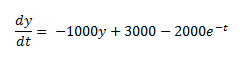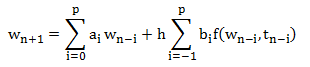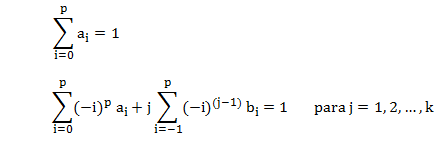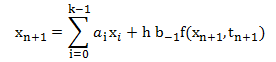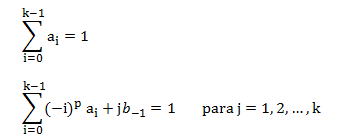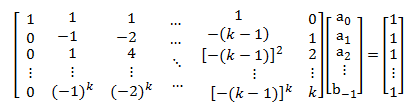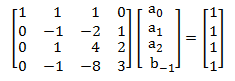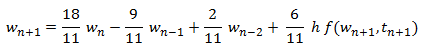Conceptos básicos

La rigidez es un problema especial que puede surgir en la solución de ecuaciones diferenciales ordinarias. Un sistema rígido es uno que tiene componentes que cambian rápidamente, junto con componentes de cambio lento. En muchos casos, los componentes de variación rápida son transitorios, desaparecen rápidamente, después de lo cual los componentes de variación lenta son los que dominan la solución. Pero, aunque el fenómeno transitorio existe en sólo un período pequeño, puede determinar el paso del tiempo en la aplicación de un método numérico.

Las ecuaciones rígidas son aquellas cuyas soluciones contienen escalas significativamente diferentes para la variable independiente. Cuando la escala más grande es la de interés, pero la escala más pequeña dicta el tamaño de paso de un método con base en la estabilidad, se dice que la ecuación es rígida.

Tanto las EDO como los sistemas de EDO pueden ser rígidos. Por ejemplo, una EDO rígida es la que se muestra a continuación:

(1)

Si se considera la condición inicial y(0) = 0, la solución analítica que se obtiene está dada por:

(2)

La solución, al principio, se encuentra dominada por el término exponencial rápido e^-1000t, después de un período muy corto (t < 0,005), esta parte transitoria termina y la solución se rige por el exponencial lento e^-t.

Analizando la parte homogénea de la ecuación (1), se puede determinar el tamaño de paso necesario para que la solución sea estable. Sea entonces la ecuación homogénea

(3)

Con la condición y(0) = y₀, se obtiene la solución que se muestra en (4), que asintóticamente se aproxima a cero, comenzando en el valor y₀.

(4)

Si se aplica el método de Euler a la ecuación (3), se obtiene la fórmula

(5)

por lo que podemos decir que y_i = y₀(1-ah)ⁱ. Para que esta solución numérica sea acotada, deberá ser |1-ah| ≤ 1. De aquí surge que si h > 2/a, entonces |y_i| crece indefinidamente cuando i tiende a infinito.

Por lo tanto, en la solución numérica de (1) mediante el método de Euler, para mantener la estabilidad, se debe tomar h ≤ 2/1000 = 0,002. Con este valor se logra estabilidad, pero para lograr precisión en la solución, se debería tomar un valor más chico de h. Si el intervalo en donde se busca la solución es grande, es claro que esta cota del paso implicará una gran cantidad de iteraciones.

La familia de los métodos multipasos de Gear se adapta particularmente bien para brindar una solución numérica de sistemas de EDO rígidos. Veamos cómo se deducen las fórmulas de estos métodos.

y también, que esta fórmula da el valor exacto para y(t_n+1) cuando y(t) es un polinomio de grado menor o igual a k si se cumplen las siguientes restricciones de exactitud (también llamadas restricciones de consistencia):

La familia de los métodos multipasos de Gear está identificada por tener todos los coeficientes b_i, excepto b_-1, nulos; en oposición a los métodos de Adams que tienen todos los coeficientes a_i nulos, excepto a₀. Obviamente, dado que b_-1 ≠ 0, los métodos de Gear son métodos implícitos.

El método de Gear de orden k se obtiene haciendo p = k-1, y b₀= b₁= b₂= ... = 0, conduciendo a la fórmula:

Los k+1 coeficientes de esta fórmula pueden obtenerse aplicando las restricciones de consistencia (8), análogamente como se hizo con los métodos de Adams, resultando:

Explicitando las ecuaciones para cada j, y desarrollando las sumatorias, se obtiene el siguiente sistema de ecuaciones:

La solución del sistema (11) determina en forma única los k+1 coeficientes necesarios para el método de Gear de orden k.

Por ejemplo, la fórmula del método de Gear de tercer orden, se obtiene resolviendo el sistema dado en (11), para el valor k = 3:

Resolviendo el sistema dado en (12), se obtienen los valores: b_-1 = 6/11, a₀ = 18/11, a₁ = -9/11 y a₂= 2/11, resultando entonces la fórmula del método:

Cuando se implementa este algoritmo, se deben guardar en memoria los valores w_n-2, w_n-1 y w_n, y se debe resolver la ecuación (13) con algún método iterativo, si la función f(y, t) es no lineal.