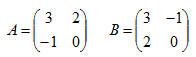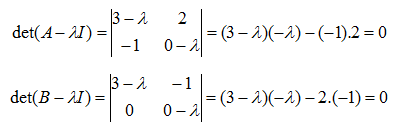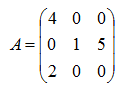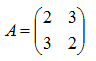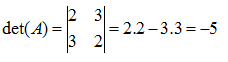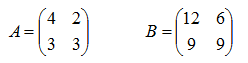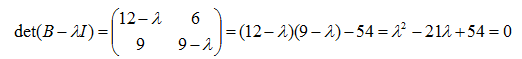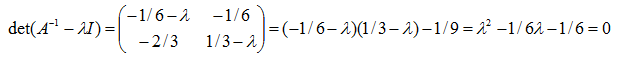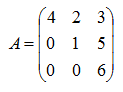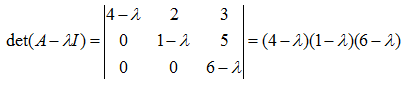Enunciaremos las propiedades, y veremos algunos ejemplos. Las demostraciones se pueden encontrar en la bibliografía citada.
ü Los autovalores de una matriz A y su transpuesta, At, coinciden. Ver ejemplo
ü Si A es una matriz de rango r, el número de autovalores nulos de una matriz de orden n es mayor o igual a n-r. Ver ejemplo
ü El determinante de una matriz A es igual al producto de sus autovalores. Ver ejemplo
ü La traza de una matriz A coincide con la suma de sus autovalores. Ver ejemplo
ü Si una matriz A tiene por autovalores l1, l2, ..., ln, entonces los autovalores de la matriz aA son al1,a l2, ..., aln. Ver ejemplo
ü Si una matriz A tiene por autovalores l1, l2, ..., ln, entonces los autovalores de la matriz inversa A-1 son 1/l1,1/ l2, ..., 1/ln. Ver ejemplo
ü Los autovalores de una matriz triangular son los elementos de la diagonal. Ver ejemplo