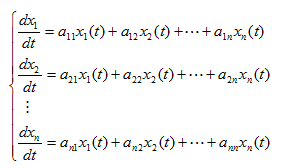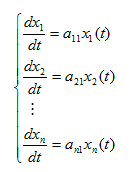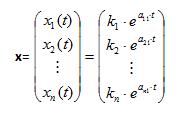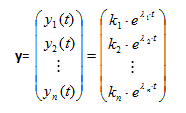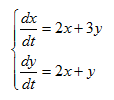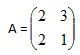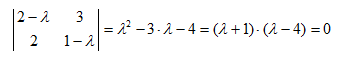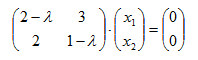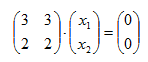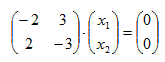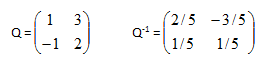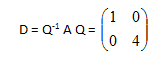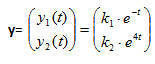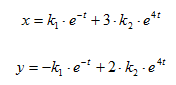Un sistema de ecuaciones diferenciales ordinarias de primer orden es aquel en que las incógnitas son funciones de una variable y en las ecuaciones aparecen las funciones y sus derivadas de primer orden. En muchos problemas de aplicación, surgen estos sistemas, donde las incógnitas son funciones que dependen del tiempo. El sistema puede ser expresado como:
|
|
(1) |
Matricialmente, dicho sistema se puede escribir
|
x´(t)= A.x(t) |
(2) |
siendo x(t) = (x1(t), x2(t),..., xn(t))t una función vectorial.
El caso más sencillo de estos sistemas es cuando el mismo está constituido por una sola ecuación diferencial, es decir:
|
x´(t)= a . x(t) |
(3) |
Multiplicando ambos
miembros esta ecuación (3) por el recíproco de x(t) e integrando
respecto de t, resulta:
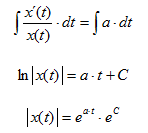
Por lo tanto, la solución general de la ecuación diferencial (3) resulta
|
x(t) = k eat |
(4) |
Si en el sistema (2) se considera A diagonal, entonces el sistema (1) se puede expresar de la forma:
|
|
(5) |
cuya solución general está dada por:
|
|
(6) |
Por lo tanto, la idea para resolver el sistema (2) es reducirlo a un
sistema con matriz diagonal, del tipo (5), diagonalizando la matriz A.
Si A es diagonalizable, entonces existe Q regular tal que D = Q-1.A.Q, por lo tanto A = Q .D.Q-1
Reemplazando la matriz A en el sistema (2) se obtiene
x´(t)= Q.D.Q-1. x(t)
Premultiplicando ambos miembros por Q-1 en la igualdad anterior, se obtiene
|
Q-1 . x´(t)= D . Q-1 . x(t) |
(7) |
Llamando y(t)= Q-1.x(t), la igualdad (7) puede escribirse de la forma:
|
y´(t) = D . y(t) |
(8) |
De la igualdad y(t)= Q-1.x(t), resulta x(t)
= Q.y(t). Por lo tanto, x´(t) = Q.y´(t) y la
solución del sistema (8) es:
|
|
(9) |
donde los son los autovalores asociados a la matriz A y que conforman la diagonal de la matriz diagonal D.
La solución del sistema (2) se obtiene de la ecuación x(t) = Q . y(t) usando los autovectores asociados a la matriz A ubicados en las columnas de Q.
| Ejemplo | |
 |
Determinar la solución del siguiente sistema de ecuaciones diferenciales:
Para obtener la solución de este sistema (10), según lo descripto más
arriba, es necesario diagonalizar la matriz de coeficientes A, siendo
Para obtener la matriz diagonal D, se calcularán los autovalores asociados a la matriz A. Para ello, se plantea el polinomio característico de dicha matriz, y se obtienen sus raíces:
Las raíces de este polinomio son λ1 = 1 y λ2 = 4.
Si λ1 = 1, resulta:
La matriz diagonal semejante a la matriz A es:
La solución del sistema y´(t) = D.y(t) = , está dada por:
Por lo tanto, la solución del sistema original es:
Otra forma de expresar esta solución, teniendo en cuenta que x = (x, y)t es:
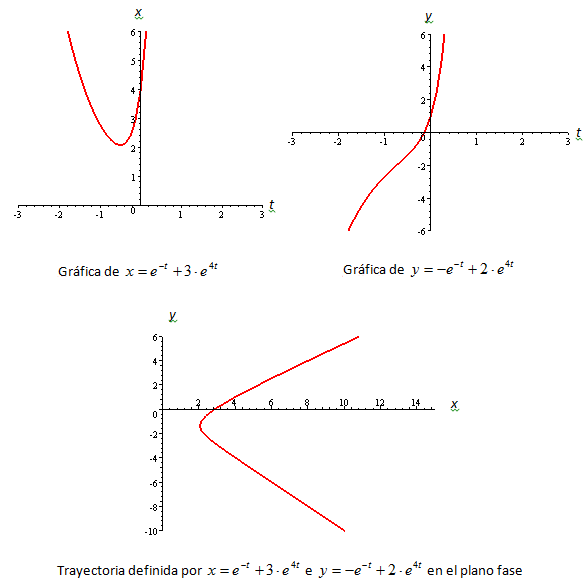
Estas ecuaciones pueden interpretarse como ecuaciones paramétricas de una curva en el plano xy, o plano fase. Cada curva, correspondiente a elecciones específicas para k1 y k2, se llama trayectoria. En la Figura 1, se muestran las tres gráficas, x(t) en el plano xt , y(t) en el plano yt y la trayectoria en el plano fase que corresponden a la elección de constantes k1 = k2 = 1 en las ecuaciones que definen x e y.
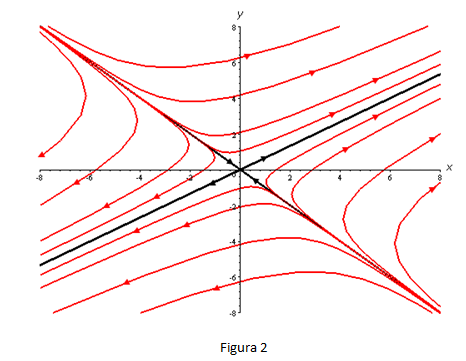
A un conjunto de trayectorias representativas en el plano de fase se le llama retrato de fase del sistema lineal dado. En la Figura 2, se muestra el retrato de fase del ejemplo analizado. El origen de coordenadas no sólo es una solución constante de todo sistema lineal homogéneo 2x2, sino también un punto importante en el estudio cualitativo de esos sistemas. Si se piensa en términos físicos, las flechas de cada trayectoria en la Figura 1 indican la dirección con que se mueve una partícula cuyas coordenadas son (x(t), y(t)) en esa trayectoria, en el instante t, a medida que aumenta el tiempo. Se puede observar que las flechas, con la sola excepción de las que hay en las semirrectas del segundo y cuarto cuadrante, indican que una partícula se aleja del origen cuando aumenta el tiempo t. Si se imagina que el tiempo transcurre de -∞ a ∞, se puede observar que una trayectoria, o una partícula en movimiento, “parte” en forma asintótica hacia una de las semirrectas definidas por (1,-1)t.e-t o por -(1,-1)t.e-t y “termina” asintóticamente en una de las semirrectas definidas por (3, 2)t.e4t y -(3,2)t.e4t .
Este es un retrato de fase característico de todos los sistemas lineales
homogéneos de 2x2 , con valores propios reales de signos opuestos. En el
caso en que los valores propios sean reales, distintos y positivos, las
flechas indican que una partícula se aleja del origen sobre cualquier
trayectoria cuando t®∞. En consecuencia, el origen es un repulsor. |